Folders
Files
DESCRIPTION
index.html
next_motif.gif
PACKAGES
previous_motif.gif
R-logo.gif
Simple_0.6.tar.gz
Simple_0.6.zip
simpleR.R
stat.html
stat001.gif
stat001.html
stat002.gif
stat002.html
stat003.gif
stat003.html
stat004.gif
stat004.html
stat005.gif
stat005.html
stat006.gif
stat006.html
stat007.gif
stat007.html
stat008.gif
stat008.html
stat009.gif
stat009.html
stat010.gif
stat010.html
stat011.gif
stat011.html
stat012.gif
stat012.html
stat013.gif
stat013.html
stat014.gif
stat014.html
stat015.gif
stat015.html
stat016.gif
stat016.html
stat017.gif
stat017.html
stat018.gif
stat018.html
stat019.gif
stat019.html
stat020.gif
stat020.html
stat021.gif
stat021.html
stat022.gif
stat022.html
stat023.gif
stat023.html
stat024.gif
stat024.html
stat025.gif
stat025.html
stat026.gif
stat026.html
stat027.gif
stat028.gif
stat029.gif
stat030.gif
stat031.gif
stat032.gif
stat033.gif
stat034.gif
stat035.gif
stat036.gif
stat037.gif
stat038.gif
stat039.gif
stat040.gif
stat041.gif
stat042.gif
stat043.gif
stat044.gif
stat045.gif
stat046.gif
stat047.gif
stat048.gif
stat049.gif
stat050.gif
stat051.gif
stat052.gif
stat053.gif
stat054.gif
stat055.gif
stat056.gif
stat057.gif
stat058.gif
stat059.gif



15 Analysis of Variance
Recall, the t-test was used to test hypotheses about the means of two independent samples. For example, to test if there is a difference between control and treatment groups. The method called analysis of variance (ANOVA) allows one to compare means for more than 2 independent samples.15.1 one-way analysis of variance
We begin with an example of one-way analysis of variance.
Example: Scholarship Grading
Suppose a school is trying to grade 300 different scholarship applications. As the job is too much work for one grader, suppose 6 are used. The scholarship committee would like to ensure that each grader is using the same grading scale, as otherwise the students aren't being treated equally. One approach to checking if the graders are using the same scale is to randomly assign each grader 50 exams and have them grade. Then compare the grades for the 6 graders knowing that the differences should be due to chance errors if the graders all grade equally.
To illustrate, suppose we have just 27 tests and 3 graders (not 300 and 6 to simplify data entry.). Furthermore, suppose the grading scale is on the range 1-5 with 5 being the best and the scores are reported as
Analysis of variance allows us to investigate if all the graders have the same mean. The R function to do the analysis of variance hypothesis test (oneway.test) requires the data to be in a different format. It wants to have the data with a single variable holding the scores, and a factor describing the grader or category. The stack command will do this for us:
More detailed information about the analysis is available through the function anova and aov as shown below.
Suppose a school is trying to grade 300 different scholarship applications. As the job is too much work for one grader, suppose 6 are used. The scholarship committee would like to ensure that each grader is using the same grading scale, as otherwise the students aren't being treated equally. One approach to checking if the graders are using the same scale is to randomly assign each grader 50 exams and have them grade. Then compare the grades for the 6 graders knowing that the differences should be due to chance errors if the graders all grade equally.
To illustrate, suppose we have just 27 tests and 3 graders (not 300 and 6 to simplify data entry.). Furthermore, suppose the grading scale is on the range 1-5 with 5 being the best and the scores are reported as
We enter this into our R session as follows and then make a data frame
grader 1 4 3 4 5 2 3 4 5 grader 2 4 4 5 5 4 5 4 4 grader 3 3 4 2 4 5 5 4 4
> x = c(4,3,4,5,2,3,4,5) > y = c(4,4,5,5,4,5,4,4) > z = c(3,4,2,4,5,5,4,4) > scores = data.frame(x,y,z) > boxplot(scores)Before beginning, we made a side-by-side boxplot which allows us to compare the three distributions. From this graph (not shown) it appears that grader 2 is different from graders 1 and 3.
Analysis of variance allows us to investigate if all the graders have the same mean. The R function to do the analysis of variance hypothesis test (oneway.test) requires the data to be in a different format. It wants to have the data with a single variable holding the scores, and a factor describing the grader or category. The stack command will do this for us:
> scores = stack(scores) # look at scores if not clear > names(scores) [1] "values" "ind"Looking at the names, we get the values in the variable values and the category in ind. To call oneway.test we need to use the model formula notation as follows
> oneway.test(values ~ ind, data=scores, var.equal=T)
One-way analysis of means
data: values and ind
F = 1.1308, num df = 2, denom df = 21, p-value = 0.3417
We see a p-value of 0.34 which means we accept the null hypothesis of
equal means.More detailed information about the analysis is available through the function anova and aov as shown below.
15.2 Analysis of variance described
The oneway test above is a hypothesis test to see if the means of the variables are all equal. Think of it as the generalization of the two-sample t-test. What are the assumptions on the data? As you guessed, the data is assumed normal and independent. However, to be clear lets give some notation. Suppose there are p variables X1, ...XP. Then each variable has data for it. Say there are nj data points for the variable Xj (these can be of different sizes). Finally, Let Xij be the ith value of the variable labeled Xj. (So in the dataframe format i is the row and j the column. This is also the usual convention for indexing a matrix.) Then we assume all of the following: Xij is normal with mean µj and variance s2. All the values in the jth column are independent of each other, and all the other columns. That is, the Xij are i.i.d. normal with common variance and mean µj.Notationally we can say
Xij = µj + eij, eij i.i.d
N(0,s2).
The one-way test is a hypothesis test that tests the null hypothesis that µ1 = µ2 = ··· = µp against that alternative that one or more means is different. That is
H0: µ1 = µ2 = ··· = µp,
HA: atleast one is not equal.
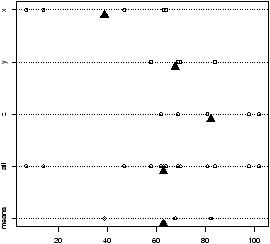
How does the test work? An example is illustrative. Figure 55 plots a stripchart of the 3 variables labeled x, y, and z. The variable x is a simulated normal with mean 40 whereas y and z have mean 60. All three have variance 102. The figure also plots a stripchart of all the numbers, and one of just the means of x, y and z. The point of this illustration16 is to show variation around the means for each row which are marked with triangles. For the upper three notice there is much less variation around their mean than for all the 3 sets of numbers considered together (the 4th row). Also notice that there is very little variation for the 3 means around the mean of all the values in the last row. We are led to believe that the large variation if row 4 is due to differences in the means of x, y and z and not just random fluctuations. If the three means were the same, then variation for all the values would be similar to the variation of any given variable. In this figure, this is clearly not so.
Analysis of variance makes this specific. How to compare the variations? ANOVA uses sums of squares. For example, for each group we have the within group sum of squares
| within SS | = |
|
|
(Xij - |
|
)2 |
|
= |
|
|
Xij. |
For all the data, one uses the grand mean, X--, (all the data averaged) to find the total sum of squares
| total SS | = |
|
|
(Xij - |
|
)2 |
Finally, the between sum of squares is the name given to the amount of variation of the means of each variable. In many applications, this is called the ``treatment'' effect. It is given by
| between SS | = |
|
|
( |
|
- |
|
)2 = |
|
nj ( |
|
- |
|
)2 = treatment SS. |
A key relationship is
total SS = within SS + between SS
Recall, the model involves i.i.d. errors with common variance s2. Each term of the within sum of squares (if normalized) estimates s2 and so this variable is an estimator for s2. As well, under the null hypothesis of equal means, the treatment sum of squares is also an estimator for s2 when properly scaled.
To compare differences between estimates for a variance, one uses the F statistic defined below. The sampling distribution is known under the null hypothesis if the data follow the specified model. It is an F distribution with (p-1,n-p) degrees of freedom.
| F = |
|
/ |
|
Some Extra Insight: Mean sum of squares
The sum of squares are divided by their respective degrees of freedom. For example, the within sum of squares uses the p estimated means Xi-- and so there are n-p degrees of freedom. This normalizing is called the mean sum of squares.
The sum of squares are divided by their respective degrees of freedom. For example, the within sum of squares uses the p estimated means Xi-- and so there are n-p degrees of freedom. This normalizing is called the mean sum of squares.
Now, we have formulas and could do all the work ourselves, but were here to learn how to let the computer do as much work for us as possible. Two functions are useful in this example: oneway.test to perform the hypothesis test, and anova to give detailed
For the data used in figure 55 the output of oneway.test yields
> df = stack(data.frame(x,y,z)) # prepare the data
> oneway.test(values ~ ind, data=df,var.equal=T)
One-way analysis of means
data: values and ind
F = 6.3612, num df = 2, denom df = 12, p-value = 0.01308
By default, it returns the value of F and the p-value but
that's it. The small p value matches our analysis of the figure.
That is the means are not equal. Notice, we set explicitly that
the variances are equal with var.equal=T.The function anova gives more detail. You need to call it on the result of lm
> anova(lm(values ~ ind, data=df))
Analysis of Variance Table
Response: values
Df Sum Sq Mean Sq F value Pr(>F)
ind 2 4876.9 2438.5 6.3612 0.01308 *
Residuals 12 4600.0 383.3
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
The row ind gives the between sum of squares. Notice, it
has p-1 degrees of freedom (p=3 here), the column Mean Sq. is just
the column Sum sq divided by the respective value of
Df. The F value is the ratio of the two mean sums of
squares, and the p-value for the hypothesis test of equal
means. Notice it is identical to that given by
oneway.test.
Some Extra Insight: Using aov
Alternatively, you could use the function aov to replace the combination of anova(lm()). However, to get a similar output you need to apply the summary command to the output of aov.
Alternatively, you could use the function aov to replace the combination of anova(lm()). However, to get a similar output you need to apply the summary command to the output of aov.
15.3 The Kruskal-Wallis test
The Kruskal-Wallis test is a nonparametric test that can be used in place of the one-way analysis of variance test if the data is not normal. It used in a similar manner as the Wilcoxen signed-rank test is used in place of the t-test. It too is a test on the ranks of the original data and so the normality of the data is not needed.The Kruskal-Wallis test will be appropriate if you don't believe the normality assumption of the oneway test. Its use in R is similar to oneway.test
> kruskal.test(values ~ ind, data=df)
Kruskal-Wallis rank sum test
data: values by ind
Kruskal-Wallis chi-squared = 6.4179, df = 2, p-value = 0.0404
You can also call it directly with a data frame as in
kruskal.test(df). Notice the p-value is small, but not
as small as the oneway ANOVA, however in both cases the null
hypothesis seems doubtful.
15.4 Problems
- 15.1
- The dataset InsectSpray has data on the count of insects in areas treated with one of 6 different types of sprays. The dataset is already in the proper format for the oneway analysis of variance -- a vector with the data (count), and one with a factor describing the level (spray). First make a side-by-side boxplot to see if the means are equal. Then perform a oneway ANOVA to check if they are. Do they agree?
- 15.2
- The simple dataset failrate contains the percentage of students failing for 7 different teachers in their recent classes. (Students might like to know who are the easy teachers). Do a one-way analysis of variance to test the hypothesis that the rates are the same for all 7 teachers. (You can still use stack even though the columns are not all the same size.) What do you conclude?
- 15.3
- (Cont.) For the failrate dataset construct a test to see if the professors V2 to V7 have the same mean failrate.
Copyright © John Verzani, 2001-2. All rights reserved.