Folders
Files
DESCRIPTION
index.html
next_motif.gif
PACKAGES
previous_motif.gif
R-logo.gif
Simple_0.6.tar.gz
Simple_0.6.zip
simpleR.R
stat.html
stat001.gif
stat001.html
stat002.gif
stat002.html
stat003.gif
stat003.html
stat004.gif
stat004.html
stat005.gif
stat005.html
stat006.gif
stat006.html
stat007.gif
stat007.html
stat008.gif
stat008.html
stat009.gif
stat009.html
stat010.gif
stat010.html
stat011.gif
stat011.html
stat012.gif
stat012.html
stat013.gif
stat013.html
stat014.gif
stat014.html
stat015.gif
stat015.html
stat016.gif
stat016.html
stat017.gif
stat017.html
stat018.gif
stat018.html
stat019.gif
stat019.html
stat020.gif
stat020.html
stat021.gif
stat021.html
stat022.gif
stat022.html
stat023.gif
stat023.html
stat024.gif
stat024.html
stat025.gif
stat025.html
stat026.gif
stat026.html
stat027.gif
stat028.gif
stat029.gif
stat030.gif
stat031.gif
stat032.gif
stat033.gif
stat034.gif
stat035.gif
stat036.gif
stat037.gif
stat038.gif
stat039.gif
stat040.gif
stat041.gif
stat042.gif
stat043.gif
stat044.gif
stat045.gif
stat046.gif
stat047.gif
stat048.gif
stat049.gif
stat050.gif
stat051.gif
stat052.gif
stat053.gif
stat054.gif
stat055.gif
stat056.gif
stat057.gif
stat058.gif
stat059.gif



12 Chi Square Tests
The chi-squared distribution allows for statistical tests of categorical data. Among these tests are those for goodness of fit and independence.12.1 The chi-squared distribution
The c2-distribution (chi-squared) is the distribution of the sum of squared normal random variables. Let Zi be i.i.d. normal(0,1) random numbers, and set| c2 = |
|
Zi2 |
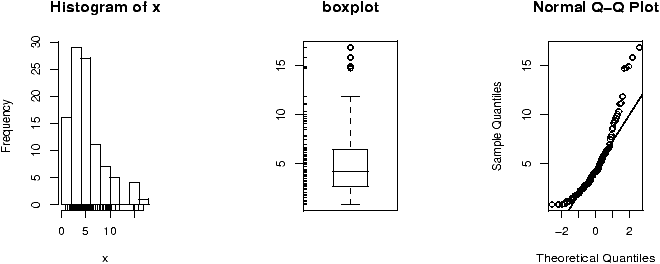
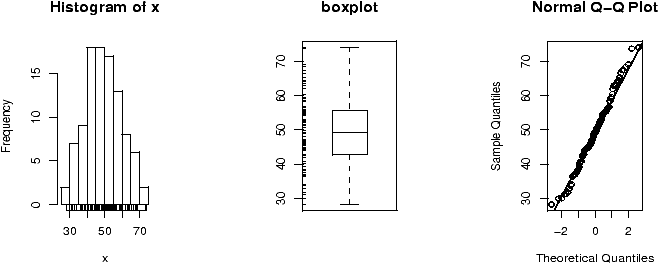
The shape of the distribution depends upon the degrees of freedom. These diagrams (figures 48 and 49) illustrate 100 random samples for 5 d.f. and 50 d.f.
> x = rchisq(100,5);y=rchisq(100,50) > simple.eda(x);simple.eda(y)
Notice for a small number of degrees of freedom it is very skewed. However, as the number gets large the distribution begins to look normal. (Can you guess the mean and standard deviation?)
12.2 Chi-squared goodness of fit tests
A goodness of fit test checks to see if the data came from some specified population. The chi-squared goodness of fit test allows one to test if categorical data corresponds to a model where the data is chosen from the categories according to some specified set of probabilities. For dice rolling, the 6 categories (faces) would be assumed to be equally likely. For a letter distribution, the assumption would be that some categories are more likely than other.
Example: Is the die fair?
If we toss a die 150 times and find that we have the following distribution of rolls is the die fair?
The key to answering this question is to look at how far off the data is from the expected. If we call fi the frequency of category i, and ei the expected count of category i, then the c2 statistic is defined to be
Intuitively this is large if there is a big discrepancy between the actual frequencies and the expected frequencies, and small if not.
Statistical inference is based on the assumption that none of the expected counts is smaller than 1 and most (80%) are bigger than 5. As well, the data must be independent and identically distributed -- that is multinomial with some specified probability distribution.
If these assumptions are satisfied, then the c2 statistic is approximately c2 distributed with n-1 degrees of freedom. The null hypothesis is that the probabilities are as specified, against the alternative that some are not.
Notice for our data, the categories all have enough entries and the assumption that the individual entries are multinomial follows from the dice rolls being independent.
R has a built in test for this type of problem. To use it we need to specify the actual frequencies, the assumed probabilities and the necessary language to get the result we want. In this case -- goodness of fit -- the usage is very simple
As we see, the value of c2 is 6.72 and the degrees of freedom are 6-1=5. The calculated p-value is 0.2423 so we have no reason to reject the hypothesis that the die is fair.
If we toss a die 150 times and find that we have the following distribution of rolls is the die fair?
Of course, you suspect that if the die is fair, the probability of each face should be the same or 1/6. In 150 rolls then you would expect each face to have about 25 appearances. Yet the 6 appears 36 times. Is this coincidence or perhaps something else?
face 1 2 3 4 5 6 Number of rolls 22 21 22 27 22 36
The key to answering this question is to look at how far off the data is from the expected. If we call fi the frequency of category i, and ei the expected count of category i, then the c2 statistic is defined to be
| c2 = |
|
|
Intuitively this is large if there is a big discrepancy between the actual frequencies and the expected frequencies, and small if not.
Statistical inference is based on the assumption that none of the expected counts is smaller than 1 and most (80%) are bigger than 5. As well, the data must be independent and identically distributed -- that is multinomial with some specified probability distribution.
If these assumptions are satisfied, then the c2 statistic is approximately c2 distributed with n-1 degrees of freedom. The null hypothesis is that the probabilities are as specified, against the alternative that some are not.
Notice for our data, the categories all have enough entries and the assumption that the individual entries are multinomial follows from the dice rolls being independent.
R has a built in test for this type of problem. To use it we need to specify the actual frequencies, the assumed probabilities and the necessary language to get the result we want. In this case -- goodness of fit -- the usage is very simple
> freq = c(22,21,22,27,22,36)
# specify probabilities, (uniform, like this, is default though)
> probs = c(1,1,1,1,1,1)/6 # or use rep(1/6,6)
> chisq.test(freq,p=probs)
Chi-squared test for given probabilities
data: freq
X-squared = 6.72, df = 5, p-value = 0.2423
The formal hypothesis test assumes the null hypothesis is that each
category i has probability pi (in our example each pi = 1/6)
against the alternative that at least one category doesn't have
this specified probability.As we see, the value of c2 is 6.72 and the degrees of freedom are 6-1=5. The calculated p-value is 0.2423 so we have no reason to reject the hypothesis that the die is fair.
Example: Letter distributions
The letter distribution of the 5 most popular letters in the English language is known to be approximately 13
The solution is just slightly more difficult, as the probabilities need to be specified. Since the assumptions of the chi-squared test require independence of each letter, this is not quite appropriate, but supposing it is we get
The letter distribution of the 5 most popular letters in the English language is known to be approximately 13
That is when either E,T,N,R,O appear, on average 29 times out of 100 it is an E and not the other 4. This information is useful in cryptography to break some basic secret codes. Suppose a text is analyzed and the number of E,T,N,R and O's are counted. The following distribution is found
letter E T N R O freq. 29 21 17 17 16
Do a chi-square goodness of fit hypothesis test to see if the letter proportions for this text are pE=.29, pT=.21, pN=.17, pR=.17, pO=.16 or are different.
letter E T N R O freq. 100 110 80 55 14
The solution is just slightly more difficult, as the probabilities need to be specified. Since the assumptions of the chi-squared test require independence of each letter, this is not quite appropriate, but supposing it is we get
> x = c(100,110,80,55,14)
> probs = c(29, 21, 17, 17, 16)/100
> chisq.test(x,p=probs)
Chi-squared test for given probabilities
data: x
X-squared = 55.3955, df = 4, p-value = 2.685e-11
This indicates that this text is unlikely to be written in English.
Some Extra Insight: Why the cs?
What makes the statistic have the c2 distribution? If we assume that fi - ei = Zi
. That is the error is
somewhat proportional to the square root of the expected number,
then if Zi are normal with mean 0 and variance 1, then the
statistic is exactly c2. For the multinomial distribution,
one needs to verify, that asymptotically, the differences from the
expected counts are roughly this large.
What makes the statistic have the c2 distribution? If we assume that fi - ei = Zi
| ( | ei | ) |
|
12.3 Chi-squared tests of independence
The same statistic can also be used to study if two rows in a contingency table are ``independent''. That is, the null hypothesis is that the rows are independent and the alternative hypothesis is that they are not independent.For example, suppose you find the following data on the severity of a crash tabulated for the cases where the passenger had a seat belt, or did not:
Are the two rows independent, or does the seat belt make a difference? Again the chi-squared statistic makes an appearance. But, what are the expected counts? Under a null hypothesis assumption of independence, we can use the marginal probabilities to calculate the expected counts. For example
Injury Level None minimal minor major Seat Belt Yes 12,813 647 359 42 No 65,963 4,000 2,642 303
P(none and yes) = P(none)P(yes)
which is estimated by the proportion of ``none'' (the column sum divided
by n) and the proportion of ``yes: (the row sum divided by n). The
expected frequency for this cell is then this product times n. Or
after simplifying, the row sum times the column sum divided by
n. We need to do this for each entry. Better to let the computer
do so. Here it is quite simple.
> yesbelt = c(12813,647,359,42)
> nobelt = c(65963,4000,2642,303)
> chisq.test(data.frame(yesbelt,nobelt))
Pearson's Chi-squared test
data: data.frame(yesbelt, nobelt)
X-squared = 59.224, df = 3, p-value = 8.61e-13
This tests the null hypothesis that the two rows are independent
against the alternative that they are not. In this example, the
extremely small p-value leads us to believe the two rows are not
independent (we reject).Notice, we needed to make a data frame of the two values. Alternatively, one can just combine the two vectors as rows using rbind.
12.4 Chi-squared tests for homogeneity
The test for independence checked to see if the rows are independent, a test for homogeneity, tests to see if the rows come from the same distribution or appear to come from different distributions. Intuitively, the proportions in each category should be about the same if the rows are from the same distribution. The chi-square statistic will again help us decide what it means to be ``close'' to the same.
Example: A difference in distributions?
The test for homogeneity tests categorical data to see if the rows come from different distributions. How good is it? Let's see by taking data from different distributions and seeing how it does.
We can easily roll a die using the sample command. Let's roll a fair one, and a biased one and see if the chi-square test can decide the difference.
First to roll the fair die 200 times and the biased one 100 times and then tabulate:
Consider how many 2's the fair die should roll in 200 rolls. The expected number would be 200 times the probability of rolling a 1. This we don't know, but if we assume that the two rows of numbers are from the same distribution, then the marginal proportions give an estimate. The marginal total is 30/300 = (26 + 4)/300 = 1/10. So we expect 200(1/10) = 20. And we had 26.
As before, we add up all of these differences squared and scale by the expected number to get a statistic:
Under the null hypothesis that both sets of data come from the same distribution (homogeneity) and a proper sample, this has the chi-squared distribution with (2-1)(6-1)=5 degrees of freedom. That is the number of rows minus 1 times the number of columns minus 1.
The heavy lifting is done for us as follows with the chisq.test function.
If you wish to see some of the intermediate steps you may. The result of the test contains more information than is printed. As an illustration, if we wanted just the expected counts we can ask with the exp value of the test
The test for homogeneity tests categorical data to see if the rows come from different distributions. How good is it? Let's see by taking data from different distributions and seeing how it does.
We can easily roll a die using the sample command. Let's roll a fair one, and a biased one and see if the chi-square test can decide the difference.
First to roll the fair die 200 times and the biased one 100 times and then tabulate:
> die.fair = sample(1:6,200,p=c(1,1,1,1,1,1)/6,replace=T)
> die.bias = sample(1:6,100,p=c(.5,.5,1,1,1,2)/6,replace=T)
> res.fair = table(die.fair);res.bias = table(die.bias)
> rbind(res.fair,res.bias)
1 2 3 4 5 6
res.fair 38 26 26 34 31 45
res.bias 12 4 17 17 18 32
Do these appear to be from the same distribution? We see that the
biased coin has more sixes and far fewer twos than we should
expect. So it clearly doesn't look so. The chi-square test for
homogeneity does a similar analysis as the chi-square test for
independence. For each cell it computes an expected amount and
then uses this to compare to the frequency. What should be
expected numbers be?Consider how many 2's the fair die should roll in 200 rolls. The expected number would be 200 times the probability of rolling a 1. This we don't know, but if we assume that the two rows of numbers are from the same distribution, then the marginal proportions give an estimate. The marginal total is 30/300 = (26 + 4)/300 = 1/10. So we expect 200(1/10) = 20. And we had 26.
As before, we add up all of these differences squared and scale by the expected number to get a statistic:
| c2 = å |
|
Under the null hypothesis that both sets of data come from the same distribution (homogeneity) and a proper sample, this has the chi-squared distribution with (2-1)(6-1)=5 degrees of freedom. That is the number of rows minus 1 times the number of columns minus 1.
The heavy lifting is done for us as follows with the chisq.test function.
> chisq.test(rbind(res.fair,res.bias))
Pearson's Chi-squared test
data: rbind(res.fair, res.bias)
X-squared = 10.7034, df = 5, p-value = 0.05759
Notice the small p-value, but by some standards we still accept
the null in this numeric example.If you wish to see some of the intermediate steps you may. The result of the test contains more information than is printed. As an illustration, if we wanted just the expected counts we can ask with the exp value of the test
> chisq.test(rbind(res.fair,res.bias))[['exp']]
1 2 3 4 5 6
res.fair 33.33333 20 28.66667 34 32.66667 51.33333
res.bias 16.66667 10 14.33333 17 16.33333 25.66667
12.5 Problems
- 12.1
- In an effort to increase student retention, many colleges have tried
block programs. Suppose 100 students are broken into two groups of
50 at random. One half are in a block program, the other half
not. The number of years in attendance is then measured. We wish to
test if the block program makes a difference in retention. The data is:
Do a test of hypothesis to decide if there is a difference between the two types of programs in terms of retention.Program 1 yr 2 yr. 3 yr 4yr 5+ yrs. Non-Block 18 15 5 8 4 Block 10 5 7 18 10
- 12.2
- A survey of drivers was taken to see if they had been in an
accident during the previous year, and if so was it a minor or major
accident. The results are tabulated by age group:
Do a chi-squared hypothesis test of homogeneity to see if there is difference in distributions based on age.
Accident Type AGE None minor major under 18 67 10 5 18-25 42 6 5 26-40 75 8 4 40-65 56 4 6 over 65 57 15 1
- 12.3
- A fish survey is done to see if the proportion of fish types is
consistent with previous years. Suppose, the 3 types of fish
recorded: parrotfish, grouper, tang are historically in a 5:3:4
proportion and in a survey the following counts are found
Do a test of hypothesis to see if this survey of fish has the same proportions as historically.Type of Fish Parrotfish Grouper Tang observed 53 22 49
- 12.4
- The R dataset UCBAdmissions contains data on
admission to UC Berkeley by gender. We wish to investigate if the
distribution of males admitted is similar to that of females.
To do so, we need to first do some spade work as the data set is presented in a complex contingency table. The ftable (flatten table) command is needed. To use it try> data(UCBAdmissions) # read in the dataset > x = ftable(UCBAdmissions) # flatten > x # what is there Dept A B C D E F Admit Gender Admitted Male 512 353 120 138 53 22 Female 89 17 202 131 94 24 Rejected Male 313 207 205 279 138 351 Female 19 8 391 244 299 317We want to compare rows 1 and 2. Treating x as a matrix, we can access these with x[1:2,].
Do a test for homogeneity between the two rows. What do you conclude? Repeat for the rejected group.
Copyright © John Verzani, 2001-2. All rights reserved.