Folders
Files
DESCRIPTION
index.html
next_motif.gif
PACKAGES
previous_motif.gif
R-logo.gif
Simple_0.6.tar.gz
Simple_0.6.zip
simpleR.R
stat.html
stat001.gif
stat001.html
stat002.gif
stat002.html
stat003.gif
stat003.html
stat004.gif
stat004.html
stat005.gif
stat005.html
stat006.gif
stat006.html
stat007.gif
stat007.html
stat008.gif
stat008.html
stat009.gif
stat009.html
stat010.gif
stat010.html
stat011.gif
stat011.html
stat012.gif
stat012.html
stat013.gif
stat013.html
stat014.gif
stat014.html
stat015.gif
stat015.html
stat016.gif
stat016.html
stat017.gif
stat017.html
stat018.gif
stat018.html
stat019.gif
stat019.html
stat020.gif
stat020.html
stat021.gif
stat021.html
stat022.gif
stat022.html
stat023.gif
stat023.html
stat024.gif
stat024.html
stat025.gif
stat025.html
stat026.gif
stat026.html
stat027.gif
stat028.gif
stat029.gif
stat030.gif
stat031.gif
stat032.gif
stat033.gif
stat034.gif
stat035.gif
stat036.gif
stat037.gif
stat038.gif
stat039.gif
stat040.gif
stat041.gif
stat042.gif
stat043.gif
stat044.gif
stat045.gif
stat046.gif
stat047.gif
stat048.gif
stat049.gif
stat050.gif
stat051.gif
stat052.gif
stat053.gif
stat054.gif
stat055.gif
stat056.gif
stat057.gif
stat058.gif
stat059.gif



6 Random Data
Although Einstein said that god does not play dice, R can. For example> sample(1:6,10,replace=T) [1] 6 4 4 3 5 2 3 3 5 4or with a function
> RollDie = function(n) sample(1:6,n,replace=T) > RollDie(5) [1] 3 6 1 2 2In fact, R can create lots of different types of random numbers ranging from familiar families of distributions to specialized ones.
6.1 Random number generators in R-- the ``r'' functions.
As we know, random numbers are described by a distribution. That is, some function which specifies the probability that a random number is in some range. For example P(a < X £ b). Often this is given by a probability density (in the continuous case) or by a function P(X=k) = f(k) in the discrete case. R will give numbers drawn from lots of different distributions. In order to use them, you only need familiarize yourselves with the parameters that are given to the functions such as a mean, or a rate. Here are examples of the most common ones. For each, a histogram is given for a random sample of size 100, and density (using the ``d'' functions) is superimposed as appropriate.- Uniform.
- Uniform numbers are ones that are "equally likely" to
be in the specified range. Often these numbers are in [0,1] for
computers, but in practice can be between [a,b] where a,b depend
upon the problem. An example might be the time you wait at a traffic
light. This might be uniform on [0,2].
> runif(1,0,2) # time at light [1] 1.490857 # also runif(1,min=0,max=2) > runif(5,0,2) # time at 5 lights [1] 0.07076444 0.01870595 0.50100158 0.61309213 0.77972391 > runif(5) # 5 random numbers in [0,1] [1] 0.1705696 0.8001335 0.9218580 0.1200221 0.1836119
The general form is runif(n,min=0,max=1) which allows you to decide how many uniform random numbers you want (n), and the range they are chosen from ([min,max])
To see the distribution with min=0 and max=1 (the default) we have> x=runif(100) # get the random numbers > hist(x,probability=TRUE,col=gray(.9),main="uniform on [0,1]") > curve(dunif(x,0,1),add=T)
The only tricky thing was plotting the histogram with a background ``color''. Notice how the dunif function was used with the curve function. - Normal.
- Normal numbers are the backbone of classical statistical theory
due to the central limit theorem The normal
distribution has two parameters a mean µ and a standard deviation
s. These are the location and spread parameters. For example,
IQs may be normally distributed with mean 100 and standard deviation
16, Human gestation may be normal with mean 280 and
standard deviation about 10 (approximately). The family of normals can be standardized
to normal with mean 0 (centered) and variance 1. This is achieved by
"standardizing" the numbers, i.e. Z=(X-µ)/s.
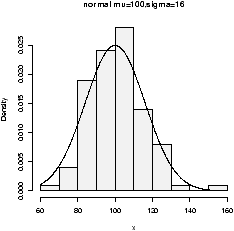
Here are some examples> rnorm(1,100,16) # an IQ score [1] 94.1719 > rnorm(1,mean=280,sd=10) [1] 270.4325 # how long for a baby (10 days early)
Here the function is called as rnorm(n,mean=0,sd=1) where one specifies the mean and the standard deviation.
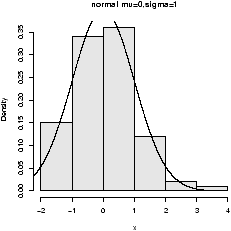
To see the shape for the defaults (mean 0, standard deviation 1) we have (figure 26)> x=rnorm(100) > hist(x,probability=TRUE,col=gray(.9),main="normal mu=0,sigma=1") > curve(dnorm(x),add=T) ## also for IQs using rnorm(100,mean=100,sd=16)
- Binomial.
- The binomial random numbers are discrete random
numbers. They have the distribution of the number of successes in
n independent Bernoulli trials where a Bernoulli trial results in
success or failure, success with probability p.
A single Bernoulli trial is given with n=1 in the binomial> n=1, p=.5 # set the probability > rbinom(1,n,p) # different each time [1] 1 > rbinom(10,n,p) # 10 different such numbers [1] 0 1 1 0 1 0 1 0 1 0
A binomially distributed number is the same as the number of 1's in n such Bernoulli numbers. For the last example, this would be 5. There are then two parameters n (the number of Bernoulli trials) and p (the success probability).
To generate binomial numbers, we simply change the value of n from 1 to the desired number of trials. For example, with 10 trials:> n = 10; p=.5 > rbinom(1,n,p) # 6 successes in 10 trials [1] 6 > rbinom(5,n,p) # 5 binomial number [1] 6 6 4 5 4
The number of successes is of course discrete, but as n gets large, the number starts to look quite normal. This is a case of the central limit theorem which states in general that (X-- - µ)/s is normal in the limit (note this is standardized as above) and in our specific case thatis approximately normal, where p^ = (number of successes)/n.^ p - p ( pq/n ) 1/2
The graphs (figure 27) show 100 binomially distributed random numbers for 3 values of n and for p=.25. Notice in the graph, as n increases the shape becomes more and more bell-shaped. These graphs were made with the commands> n=5;p=.25 # change as appropriate > x=rbinom(100,n,p) # 100 random numbers > hist(x,probability=TRUE,) ## use points, not curve as dbinom wants integers only for x > xvals=0:n;points(xvals,dbinom(xvals,n,p),type="h",lwd=3) > points(xvals,dbinom(xvals,n,p),type="p",lwd=3) ... repeat with n=15, n=50
- Exponential
- The exponential distribution is important for
theoretical work. It is used to describe lifetimes of
electrical components (to first order). For example, if the mean
life of a light bulb is 2500 hours one may think its lifetime is
random with exponential distribution having mean 2500. The one
parameter is the rate = 1/mean. We specify it as follows
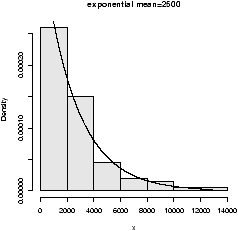
rexp(n,rate=1). Here is an example with the rate being
1/2500 (figure 28).
> x=rexp(100,1/2500) > hist(x,probability=TRUE,col=gray(.9),main="exponential mean=2500") > curve(dexp(x,1/2500),add=T)
6.2 Sampling with and without replacement using sample
R has the ability to sample with and without replacement. That is, choose at random from a collection of things such as the numbers 1 through 6 in the dice rolling example. The sampling can be done with replacement (like dice rolling) or without replacement (like a lottery). By default sample samples without replacement each object having equal chance of being picked. You need to specify replace=TRUE if you want to sample with replacement. Furthermore, you can specify separate probabilities for each if desired.Here are some examples
## Roll a die
> sample(1:6,10,replace=TRUE)
[1] 5 1 5 3 3 4 5 4 2 1 # no sixes!
## toss a coin
> sample(c("H","T"),10,replace=TRUE)
[1] "H" "H" "T" "T" "T" "T" "H" "H" "T" "T"
## pick 6 of 54 (a lottery)
> sample(1:54,6) # no replacement
[1] 6 39 23 35 25 26
## pick a card. (Fancy! Uses paste, rep)
> cards = paste(rep(c("A",2:10,"J","Q","K"),4),c("H","D","S","C"))
> sample(cards,5) # a pair of jacks, no replacement
[1] "J D" "5 C" "A S" "2 D" "J H"
## roll 2 die. Even fancier
> dice = as.vector(outer(1:6,1:6,paste))
> sample(dice,5,replace=TRUE) # replace when rolling dice
[1] "1 1" "4 1" "6 3" "4 4" "2 6"
The last two illustrate things that can be done with a little typing
and a lot of thinking using the fun commands paste for pasting
together strings, rep for repeating things and outer for
generating all possible products.
6.3 A bootstrap sample
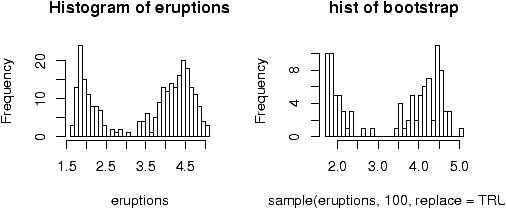
Bootstrapping is a method of sampling from a data set to make statistical inference. The intuitive idea is that by sampling, one can get an idea of the variability in the data. The process involves repeatedly selecting samples and then forming a statistic. Here is a simple illustration on obtaining a sample.The built in data set faithful has a variable ``eruptions'' that measures the time between eruptions at Old Faithful. It has an unusual distribution. A bootstrap sample is just a sample with replacement from the given values. It can be found as follows
> data(faithful) # part of R's base > names(faithful) # find the names for faithful [1] "eruptions" "waiting" > eruptions = faithful[['eruptions']] # or attach and detach faithful > sample(eruptions,10,replace=TRUE) [1] 2.03 4.37 4.80 1.98 4.32 2.18 4.80 4.90 4.03 4.70 > hist(eruptions,breaks=25) # the dataset ## the bootstrap sample > hist(sample(eruptions,100,replace=TRUE),breaks=25)
Notice that the bootstrap sample has a similar histogram, but it is different (figure 29).
6.4 d, p and q functions
The d functions were used to plot the theoretical densities above. As with the ``r'' functions, you need to specify the parameters, but differently, you need to specify the x values (not the number of random numbers n).The p and q functions are for the cumulative distribution functions and the quantiles. As mentioned, the distribution of a random number is specified by the probability that the number is between a and b for arbitrary a and b, P(a < X £ b). In fact, the value F(x) = P(X £ b) is enough.
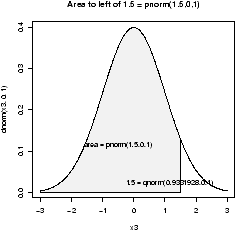
The p functions answer what is the probability that a random variable is less than x. Such as for a standard normal, what is the probability it is less than .7?
> pnorm(.7) # standard normal [1] 0.7580363 > pnorm(.7,1,1) # normal mean 1, std 1 [1] 0.3820886Notationally, these answer P(Z £ .7) where Z is a standard normal or normal(1,1). To answer P(Z > .7) is also easy. You can do the work by noting this is 1 - P(Z £ .7) or let R do the work, by specifying lower.tail=F as in:
> pnorm(.7,lower.tail=F) [1] 0.2419637The q function are inverse to this. They ask, what value corresponds to a given probability. This the quantile or point in the data that splits it accordingly. For example, what value of z has .75 of the area to the right for a standard normal? (This is Q3)
> qnorm(.75) [1] 0.6744898Notationally, this is finding z which solves 0.75 = P(Z £ z).
6.5 Standardizing, scale and z scores
To standardize a random variable you subtract the mean and then divide by the standard deviation. That is| Z = |
|
. |
You can also standardize a sample. There is a convenient function scale that will do this for you. This will make your sample have mean 0 and standard deviation 1. This is useful for comparing random variables which live on different scales.
Normal random variables are often standardized as the distribution of the standardized normal variable is again normal with mean 0 and variance 1. (The ``standard'' normal.) The z-score of a normal number is the value of it after standardizing.
If we have normal data with mean 100 and standard deviation 16 then the following will find the z-scores
> x = rnorm(5,100,16) > > x [1] 93.45616 83.20455 64.07261 90.85523 63.55869 > z = (x-100)/16 > z [1] -0.4089897 -1.0497155 -2.2454620 -0.5715479 -2.2775819The z-score is used to look up the probability of being to the right of the value of x for the given random variable. This way only one table of normal numbers is needed. With R, this is not necessary. We can use the pnorm function directly
> pnorm(z) [1] 0.34127360 0.14692447 0.01236925 0.28381416 0.01137575 > pnorm(x,100,16) # enter in parameters [1] 0.34127360 0.14692447 0.01236925 0.28381416 0.01137575
6.6 Problems
- 6.1
- Generate 10 random numbers from a uniform distribution on [0,10]. Use R to find the maximum and minimum values.x
- 6.2
- Generate 10 random normal numbers with mean 5 and standard deviation 5 (normal(5,5)). How many are less than 0? (Use R)
- 6.3
- Generate 100 random normal numbers with mean 100 and standard deviation 10. How many are 2 standard deviations from the mean (smaller than 80 or bigger than 120)?
- 6.4
- Toss a fair coin 50 times (using R). How many heads do you have?
- 6.5
- Roll a ``die'' 100 times. How many 6's did you see?
- 6.6
- Select 6 numbers from a lottery containing 49 balls. What is the largest number? What is the smallest? Answer these using R.
- 6.7
- For normal(0,1), find a number z* solving P(Z £ z*) = .05 (use qnorm).
- 6.8
- For normal(0,1), find a number z* solving P(-z* £ Z £ z*) = .05 (use qnorm and symmetry).
- 6.9
- How much area (probability) is to the right of 1.5 for a normal(0,2)?
- 6.10
- Make a histogram of 100 exponential numbers with mean 10. Estimate the median. Is it more or less than the mean?
- 6.11
- Can you figure out what this R command does?
> rnorm(5,mean=0,sd=1:5)
- 6.12
- Use R to pick 5 cards from a deck of 52. Did you get a pair or better? Repeat until you do. How long did it take?
Copyright © John Verzani, 2001-2. All rights reserved.