Basic information about spheres

We will start with the basics. A sphere is a set of points in three dimensional space equidistant from a point called the center of the sphere. The distance from the center to the points on the sphere is called the radius of the sphere. Notice that we are talking about the surface of a ball, and not the ball itself. The surface of the earth we live on is a good approximation to a sphere. As you read through this material it would be helpful to have a beach ball about 12'' in diameter with a smooth, solid colored surface, a marking pen, preferably the kind that easily washes off, string, scissors, and a protractor.

Lines and spheres.

If we take an arbitrary line and a sphere in three space, several things can happen. First, the line and the sphere can miss each other. That case is not very interesting. Secondly, the line can intersect the sphere in only one point. In that case the line is tangent to the sphere. The only other thing that can happen is that the line hits the sphere in precisely two points. In particular a line cannot lie in the sphere.

The case which is most interesting is when the line passes through the center of the sphere. In this case the two points of intersection with the sphere are said to be antipodal points. The best known example of antipodal points is the north and south poles on the earth.

Planes, spheres, circles, and great circles.

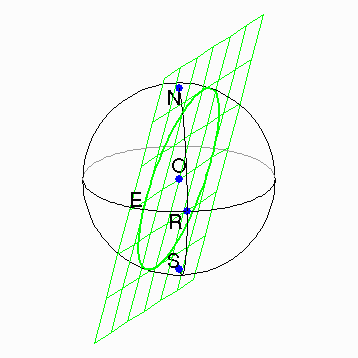It is easy to see that the circle of intersection will be largest when the plane passes through the center of the sphere, as it does in the figure to the left. Such a circle is called a great circle. A geographic example of a great circle is the equator. The meridians of longitude form exactly half a great circle. The parallels of latitude are small circles, except for the equator.

Great circles become more important when we realize that the shortest distance between two points on the sphere is along the segment of the great circle joining them. On any surface the curves that minimize the distance between points are called geodesics. Thus lines are the geodesics on the plane, and great circles fill that role on the sphere.

A pretty good approximation to a great circle can be drawn through two points on a beach ball by holding a piece of string tight to the ball at the two points in question. The tightness of the string has the effect of minimizing the length of the string, and therefore closely approximating a geodesic.

We now have the beginnings of a geometry on the sphere. In plane geometry the basic concepts are points and lines. On the sphere we have points, of course, but no lines as such. However, since the great circles are geodesics on the sphere, just as lines are in the plane, we should consider the great circles as replacements for lines. We can then compare the two geometries.

Exercise:

Take your favorite geometry book, and find its list of axioms. Which of the axioms are true for the sphere? If a planar axiom is not literally true on the sphere try to rephrase it so it is true.

This exercise cannot be completed at this point. It is one that will continue throughout this material. At this point you should check the axioms of incidence. Remember that a great circle is the intersection of the sphere with a plane that passes through the center of the sphere. Almost every fact we will discover about great circles will follow from that fact.

	The next section contains a discussion of incidence on the sphere.
	You can find a discussion of incidence relations in the plane and in space here.
	Table of Contents.