Geometry of the Sphere 2.

Incidence Relations on a Sphere.

Suppose we have two distinct points A and B on the sphere. Together with C, the center of the sphere, we have three points in space, and there are two possibilities. First suppose that A and B are not antipodal points. Then A, B, and C do not lie on the same line in space, and consequently determine a unique plane. This plane passes through C, the center of the sphere, and consequently the intersection of the plane with the sphere is a great circle containing A and B. Thus A and B determine a unique great circle.

If A and B are antipodal points, then A, B, and C lie on the same line in space. Any plane which contains this line determines a great circle which must contain A and B. Thus there are infinitely many great circles containing A and B if they are antipodal.

To sum up, the first incidence relation for the sphere is:

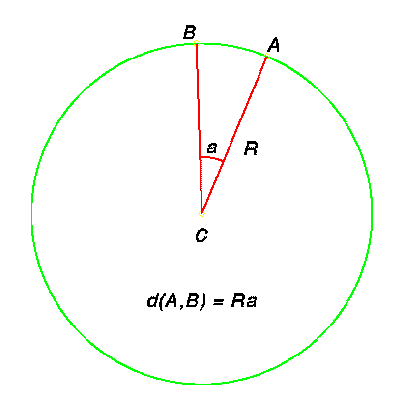If A and B are two points which are not antipodal, then there is a unique great circle that contains both of them. If A and B are antipodal, then there are infinitely many great circles conatining them.

Now suppose we have two great circles. Each of these is the intersection of the sphere with a plane through the center. These planes must intersect in a line in space, which of course interesects the sphere in two antipodal points. Thus the second incidence relation is:

Two distinct great circles meet in exactly two antipodal points.

Here is an easy question that you should be able answer. Are there parallel great circles on a sphere? To answer you will need to decide what parallel means on the sphere.

Spherical distance and isometries.

If A and B are two points on the sphere, then the distance between them is the distance along the great circle connecting them. Since this circle lies totally in a plane, we can figure this distance using the plane figure to our left. If the angle ACB is a, and if a is measured in radians, then the distance between A and B is given by

d(A,B) = R a,

where R is the radius of the sphere.

An isometry of the sphere is a mapping of the sphere to itself which preserves the distance between points. It is easy to see that a rotation of the sphere around one of the sphere's diameters is an isometry. It simply rotates the picture to the left into another one just like it, but in a different plane.

Another example of an isometry is the antipodal map, which maps a point onto the point on the other side of the sphere. In other words, given a point A on the sphere, its image under the antipodal map is the other intersection of the line AC through the point A and the center of the sphere C, with the sphere.

Lunes

In the plane the simplest polygon is the triangle. There are no interesting polygons with only two sides. This is not true on the sphere. Any two great circles meet in two antipodal points, and divide the sphere into four regions each of which has two sides which are segments of great circles. We will call such a region a lune, or a biangle.

Why is it called a lune? The name comes from the Latin word luna, which means moon. Think about the part of the moon that is seen at any time. That portion has to be in the hemisphere which is illuminated by the sun, and in the hemisphere that is visible from the earth. The intersection of two hemispheres is precisely a lune.

Lunes are pretty simple things. However there are two things we should notice about them.

The vertices of a lune are antipodal points.
The two angles of a lune are equal.

Angles on the sphere

What do we mean by an angle on the sphere? How do we measure them? After all curves on a sphere do not lie in a plane. However, the lines that are tangent to the two intersecting curves are both in the plane that is tangent to the sphere at the point of intersection. We define the angle between two curves to be the angle between the tangent lines.

We should mention that in these notes all angles will be measured in radians.

With a protractor and a little practise it is possible to measure spherical angles pretty accurately. In the case of a lune, the angle between the great circles at either of the vertices is simply the angle between the planes that define the great circles, and so it does not matter at which vertex the measurement is made.

	The next section contains a discussion of area on the sphere.
	The previous section discusses the basic properties of spheres.
	Table of Contents.

url: http://math.rice.edu/~pcmi/sphere/gos2.html

John C. Polking <polking@rice.edu>

Last modified: Thu Apr 15 09:20:24 Central Daylight Time 1999