|
|
| Advection of Tracers |
A very common example for mixing is to stir cream in a cup of coffee.
We expect that, after a couple of motions, both fluids, cream and
coffee, will have mixed homogeneously and we would be surprised to
observe something different. In 1994, Pierrehumbert considered a very
similar mixing problem: He put tracers into a fluid that was stirred
periodically expecting that the tracers will mix homogeneously. But
something different happened: The tracer concentration started to form
complex patterns that, once their formation is completed, decay
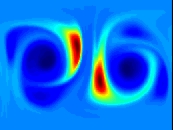
slowly. The figure below shows examples of these patterns, often
called strange eigenmodes,
whose occurrence has been confirmed many times both experimentally and
numerically. Their description is crucial for understanding any
mixing process in fluids, from small scales, e.g. drugs that are
mixing with blood being pumped periodically through the body, to large
scales, e.g. contaminants in geophysical flows such as the ocean.
Although the existence of strange eigenmodes can be shown
mathematically (see Liu-Haller, 2004), their actual structure and their
properties are not well-understood. The aim of this research project is
to provide a theory that will be able to describe both their formation
and evolution in time. This research is a collaboration with Andrew
Poje and Bala Sundaram.
Read more:
T.Schäfer, A. C. Poje, J. Vukadinovic: Averaged dynamics of time-periodic advection diffusion equations in the limit of small diffusivity. Physica D 238 (2009) 233-240.
R. T. Pierrehumbert: Tracer
microstructure in the large-eddy dominated regime, Solitons Fract, 4:1091--1110, 1994.
|
 |
|
|


