Reinforcement Learning

Machine Learning often draws on analogies from human learning to create algorithms and paradigms.

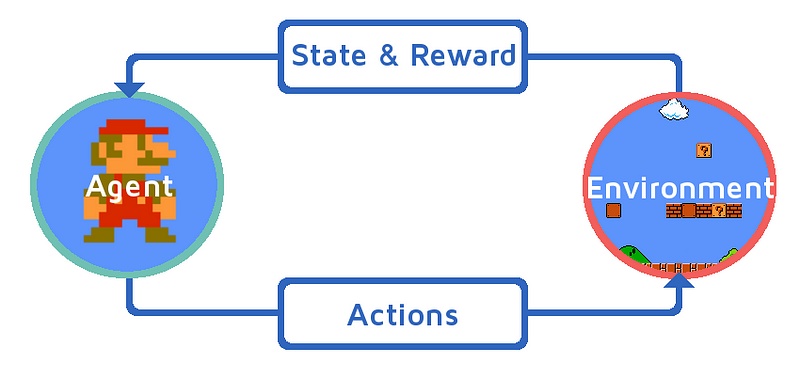
Reinforcement learning draws on the process of trial and error: the algorithm tries an action, gets a reward, and updates its decision process accordingly.

Reinforcement Learning

This approach has found applications in robotic motion planning, in game play, and other areas. Alpha Go beat a a professional player, and OpenAI beat a professional DOTA player - both with Reinforcement Learning approaches.

 

Reinforcement Learning

The formal setup is: some Agent uses some decision process to choose an action based on some observed state of its environment. The action updates the environment, and is assigned some reward. A positive reward encourages that action, a negative reward discourages it.

The objective is to maximize the accumulated reward.

In most settings, especially if there is uncertainty in the environment, it is sensible to discount this accumulated reward: rewards that take several actions to reach are worth less than immediate rewards.

$$ G_t = \sum_k \gamma^k R_{t+k+1} = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} \dots $$

Tradeoff

An important tradeoff in Reinforcement Learning is between exploration (trying new things) and exploitation (using known good strategies)

Q-Learning

A particularly interesting form of Reinforcement Learning is Q-Learning. In Q-learning, we posit a quality function $Q:S\times A \to R$ that maps each pair (state, action) to its maximum expected future accumulated rewards $Q(s,a)$.

Clearly, if we had $Q$, we could pick the action that maximizes $Q$ at any given state.

Q-Learning

At the start, we make $Q$ either constant 0, or completely random. We then update $Q$ for each achieved reward.

Given a learning rate $\alpha$, a discount factor $\gamma$, current state $s$, chosen action $a$, and updated state $s'$, the update step is

$$ Q(s,a) = \color{blue}{Q(s,a)} + \alpha\left[ \color{red}{R(s,a)} + \color{purple}{\gamma} \color{green}{\max_{a'}Q(s',a')} - \color{blue}{Q(s,a)} \right] $$

In words, the new value for $Q(s,a)$ is adjusted by adding a fraction of how much better the reward and discounted expected future rewards are than the current estimate for that action at that state.

Deep Q-Learning

Instead of explicitly estimating $Q(s,a)$, we could train a neural network to estimate $Q(s,a)$.

This simplifies the setup in that the learning rate updates are handled by the backpropagation and gradient descent optimizer.

Exploration

When exploring, the agent collects experiences: (old state, action, reward, new state)

Training

Given a batch of experiences, the model can be improved from each experience $(s,a,r,s')$ by

1. Estimate $Q(s,a)$ for all possible next actions $a$
2. Estimate $Q(s',a')$ for all possible next actions $a'$
3. Calculate new target value $Q'(s,a) = r + \gamma\max_{a'}Q(s',a')$
4. Train the network with input $s$ and output $Q'(s,a)$ for all possible $a$

This training step retains all the predicted values except the one in the experience.