Lecture 12: Manifolds, Dimensionality Reduction

Historical Timeseries: Ryan McNeil

Historical Timeseries: Paul Ayamah

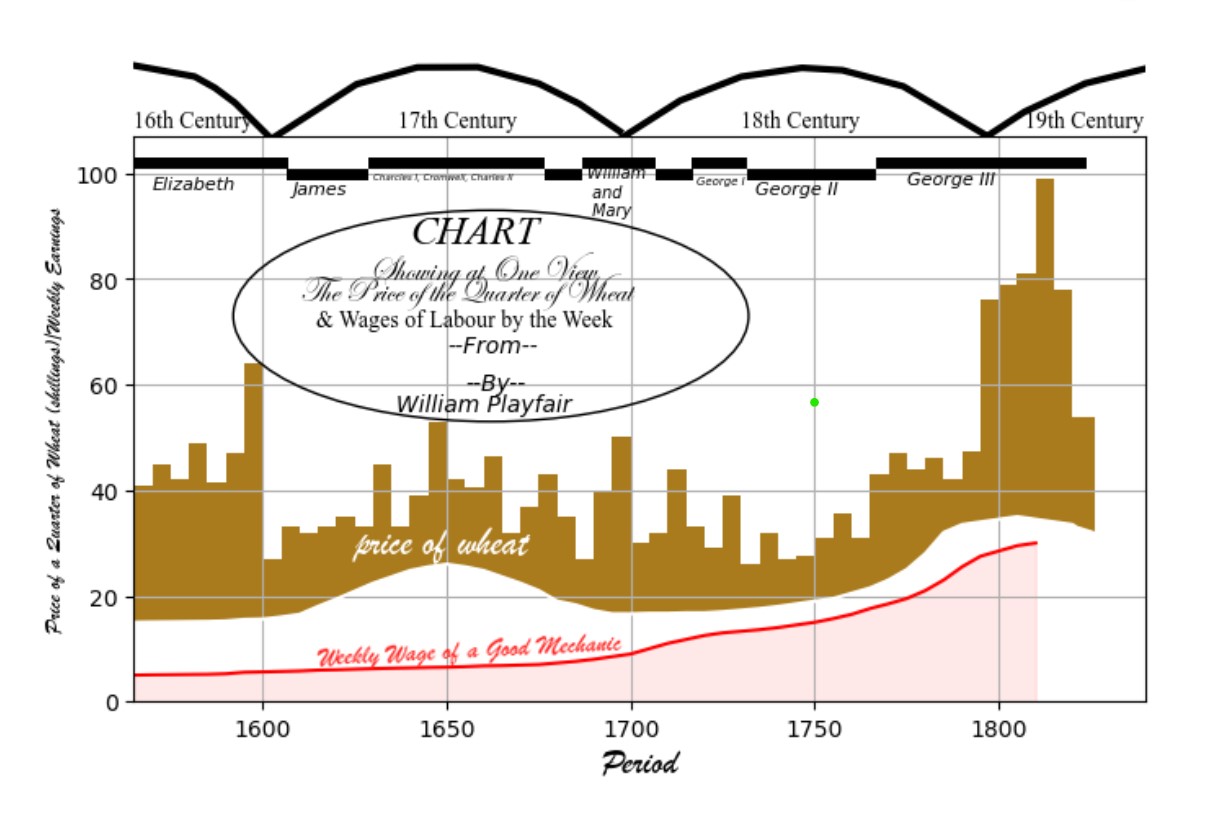
Historical Timeseries: Neh Majmudar

Historical Timeseries: Sean Sudol

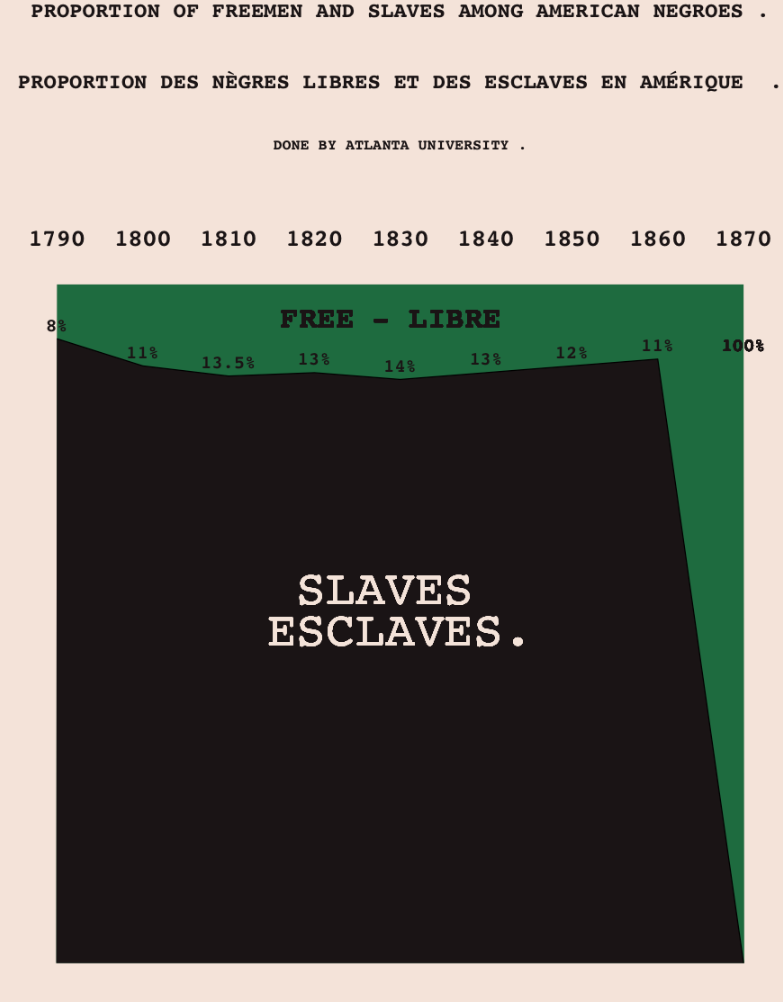
Historical Timeseries: Giacomo Radaelli

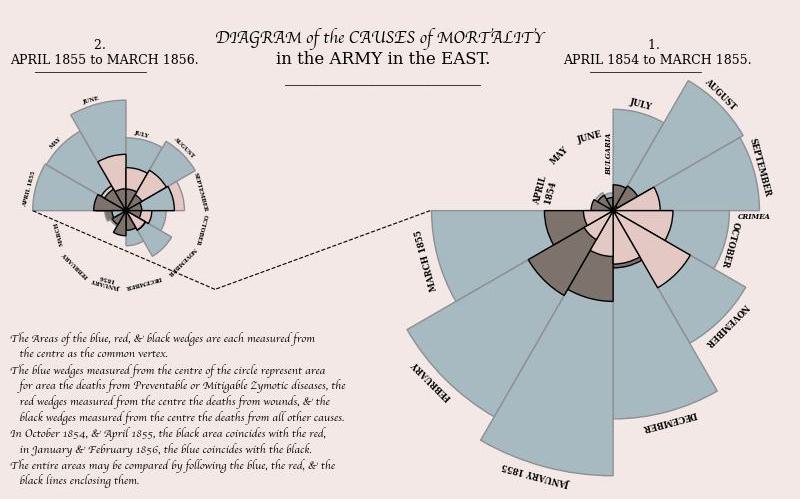
Historical Timeseries: Joshua Rollins

Historical Timeseries: Jordan Matuszewski

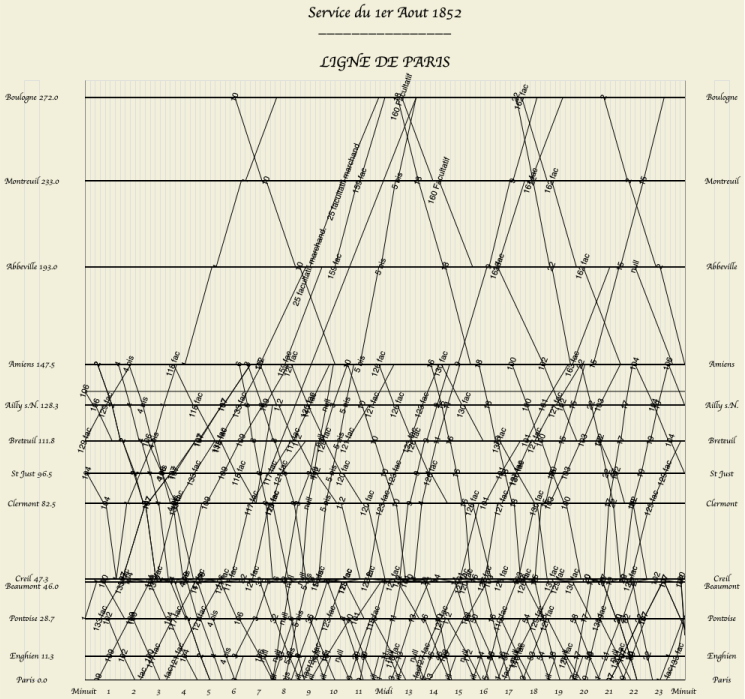
Historical Timeseries: Garima Goyal

Manifold Learning

Manifolds

Formal Definition

A topological space¹ is a manifold if it can be equipped with an atlas: a cover² where each element of the cover is homeomorphic³ to (an open subset of) \(\mathbb{R}^n\).

Intuitive Description

A shape is a manifold if it has the same dimension everywhere and neither self-intersections, nor boundaries, nor other kinds of pathological behavior.

Manifolds are a particular way of defining what it means for a shape to be nice in a theoretical sense

1. set with notion of nearness

2. a set of subsets whose union is the entire thing

3. indistinguishable with the tools of topology

The Manifold Hypothesis

Geometric/Topological machine learning and data science operate under the manifold hypothesis: an assumption that data typically lies on (or near) a relatively low-dimensional manifold embedded in a higher-dimensional ambient space.

Example: Linear Regression assumes data lies near a hyperplane.

If we can shift from ambient dimension to intrinsic dimension it may be a lot easier to work with the data.

For visualization purposes, it would be best to get down to the range of 2-5 actually relevant dimensions, to limit the number of visual channels we need to use.

Dimensionality Reduction

Dealing with high-dimensional data

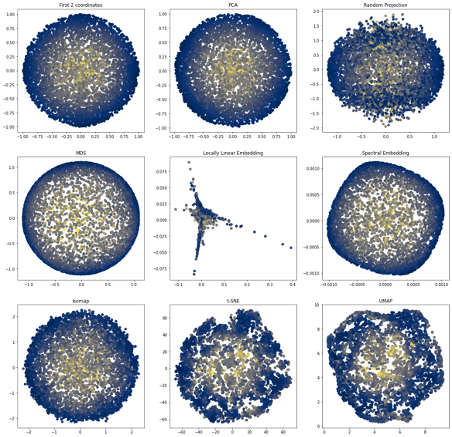
A selection of Dimensionality Reduction methods

PCA - Principal Component Analysis

Use eigenvectors of the sample covariance matrix of the data to find a linear change of basis that concentrates variability into a few basis vectors.

MDS - Multi-Dimensional Scaling

Use optimization of a stress value (sum-of-squares of differences between distances before projecting and distances after projecting) to find a map as close to isometric as possible.

Random Projection

Create a random projection matrix by generating a set of orthonormal random vectors and multiply data matrix with the projection matrix.

Johnson-Lindenstrauss Lemma: If your target dimension is \(d>8\log(N)/\epsilon^2\), then there is some map \(f\) whose squared norm distortion is no more than \(\epsilon\).

Time to read

Divide into three groups.

Each group picks one (a different one) of:

• Isomap: Tenenbaum, de Silva, Langford, A global geometric framework for nonlinear dimensionality reduction, Science 290 (2000) pp 2319-2323. http://doi.org/10.1126/science.290.5500.2319
• t-SNE: van der Maaten, Hinton, Visualizing data using t-SNE, JMLR, 9 (2008) pp 2579-2605 http://jmlr.org/papers/volume9/vandermaaten08a/vandermaaten08a.pdf
• UMAP: McInnes, Healy, Melville, Uniform manifold approximation and projection for dimension reduction, arXiv:1802.03426 https://arxiv.org/pdf/1802.03426.pdf

1. Everyone reads their article alone.
2. Discuss within your article group. Make sure everyone in your group understand the method and what distinguishes it.
3. Divide into groups of 3 (one from each group) and explain your paper to the other 2.

Dimensionality Reduction in Action

From a database (collected by van Hateren) of naturally occurring images, draw 3x3 pixel patches at random.

Most such pixel patches will be almost constant - discard those.

D Mumford et al. used PCA to identify a primary circle of high density in this data. Turns out to trace linear gradients in different orientations.

G Carlsson et al. used Topological Data Analysis to study the high-density structure more carefully. They identify a high-density Klein bottle in the data, with a direct correspondence to quadratic gradients (ridges and valleys) in different orientations.

Homework

Read https://handsondataviz.org/how-to-lie-with-charts.html