Tuesday, Thursday 4:40 p.m. – 6:20 p.m. 1S 102
Dr. Andras Balogh
1S 223 and through Zoom at (click here to get the Zoom link)
Tuesday, Thursday: 9:00 a.m. – 10:00 a.m. and 3:00 p.m. – 4:30 p.m., or by appointment. Feel free to email me if you’d like to discuss course related topics outside of office hours. There is absolutely no reason not to contact me for help.
Rogawski, Adams & Franzosa, Calculus: Early Transcendentals, 4th Edition. W. H. Freeman & Co. (2019). ISBN: 9781319050740 (e-book ISBN: 9781319055905)
Rogawski and Adams, Calculus: Early Transcendentals, 3rd Edition. W. H. Freeman & Co. (2015). ISBN# 9781464114885
This textbook is used also for MTH 232, 233. If you are only taking MTH 230 or 231 you may use Rogawski and Adams, Single Variable Calculus: Early Transcendentals.
The first of a three–semester sequence in calculus. Topics include limits, derivatives, rules of differentiation, trigonometric functions and their derivatives, differentials, graph sketching, maximum and minimum problems, related rates, antiderivatives, areas, exponential and logarithmic functions.
MTH 123 (College Algebra and Trigonometry) with a grade of A or MTH 130 (Precalculus) or an appropriate math placement or permission of the Department of Mathematics.
MTH 229 (Calculus Computer Laboratory).
Online homework will be assigned regularly through the free online homework system WeBWorK for each section of the book. Here is the link to the WeBWorK section: https://www.math.csi.cuny.edu/webwork2/Math231_28438_Balogh_F25. You can also find the link to WeBWorK in Brightspace. Typically, there will be a homework assignment due every day. There is an automatic 30% reduction in grade for late homework.
-
Students are required to have reliable internet access for accessing the homework system. This can be done even from smartphones, but a tablet or laptop or desktop computer is recommended.
There will be three midterm exams and a comprehensive final exam. All questions on all exams are open ended. On all problems, you must show your work. Write clearly and show all your work; a correct answer alone may not receive any credit. The dates for the exams will be announced at least a week in advance. All students are expected to take the examinations on the announced date.
No make-up exams will be accepted without prior approval of the instructor.
Three in–class exams: 45% (15% each); Comprehensive final: 20%; Homework (online through WeBWorK) 20%; Quizzes: 15%.
![[90%, 100% ]](HTML_MTH_2310x.png) :A;
:A; 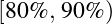 :B;
:B; 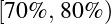 :C;
:C; 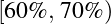 :D;
:D; 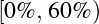 :F
:F
Below, each lesson corresponds to a one-hour class. Homework problems in bold correspond to similar WeBWorK problems, which must be submitted online. The problem numbers not in bold are for practice.