Tuesday, Thursday 10:10 a.m. – 12:05 p.m., 3S 118
Dr. Andras Balogh
(718) 982-3619
1S 223 and through Zoom at (click here to get the Zoom link)
Tuesday, Thursday: 9:00 a.m. – 10:00 a.m. and 3:00 p.m. – 4:30 p.m., or by appointment. Feel free to email me if you’d like to discuss course related topics outside of office hours. There is absolutely no reason not to contact me for help.
Stewart, Redlin, Watson, Precalculus: Mathematics for Calculus, 7th Edition with WebAssign. Brooks/Cole, Cengage Learning (2015). ISBN# 978-1305071759. The homework link in Brightspace will take you to the WebAssign page.
Topics in algebra, including inequalities, logarithmic, exponential, trigonometric functions, graphs and equations, inverse functions, elements of analytic geometry. Introduction to the use of graphing calculators.
MTH 30 (Intermediate Algebra) or an appropriate math placement or permission of the Department of Mathematics
Online homework will be assigned regularly through the online homework system WebAssign for each section of the book that we cover. You will find the link to WebAssign in Brightspace.
-
A graphing calculator is required. The TI-84 is highly recommended.
-
Students are required to have reliable internet access for accessing the homework system. This can be done even from smartphones, but a tablet or laptop or desktop computer is recommended.
There will be three midterm exams and a comprehensive final exam. All questions on all exams are open ended. Check the dates for the midterm exams. All students are expected to take the examinations on the announced date. On all problems, you must show your work. Write clearly and show all your work; a correct answer alone may not receive any credit. The dates for the exams will be announced at least a week in advance.
No make-up exams will be accepted without prior approval of the instructor.
Three in–class exams: 45% (15% each); Comprehensive final: 20%; Homework (online through WebAssign) 20%; Quizzes: 15%.
![[90%, 100% ]](HTML_MTH_1230x.png) :A;
:A; 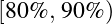 :B;
:B; 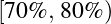 :C;
:C; 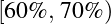 :D;
:D; 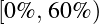 :F
:F
Below, each lesson corresponds to a one-hour class. Homework problems in bold correspond to similar WebAssign problems, which must be submitted online.