Folders
Files
DESCRIPTION
index.html
next_motif.gif
PACKAGES
previous_motif.gif
R-logo.gif
Simple_0.6.tar.gz
Simple_0.6.zip
simpleR.R
stat.html
stat001.gif
stat001.html
stat002.gif
stat002.html
stat003.gif
stat003.html
stat004.gif
stat004.html
stat005.gif
stat005.html
stat006.gif
stat006.html
stat007.gif
stat007.html
stat008.gif
stat008.html
stat009.gif
stat009.html
stat010.gif
stat010.html
stat011.gif
stat011.html
stat012.gif
stat012.html
stat013.gif
stat013.html
stat014.gif
stat014.html
stat015.gif
stat015.html
stat016.gif
stat016.html
stat017.gif
stat017.html
stat018.gif
stat018.html
stat019.gif
stat019.html
stat020.gif
stat020.html
stat021.gif
stat021.html
stat022.gif
stat022.html
stat023.gif
stat023.html
stat024.gif
stat024.html
stat025.gif
stat025.html
stat026.gif
stat026.html
stat027.gif
stat028.gif
stat029.gif
stat030.gif
stat031.gif
stat032.gif
stat033.gif
stat034.gif
stat035.gif
stat036.gif
stat037.gif
stat038.gif
stat039.gif
stat040.gif
stat041.gif
stat042.gif
stat043.gif
stat044.gif
stat045.gif
stat046.gif
stat047.gif
stat048.gif
stat049.gif
stat050.gif
stat051.gif
stat052.gif
stat053.gif
stat054.gif
stat055.gif
stat056.gif
stat057.gif
stat058.gif
stat059.gif



14 Multiple Linear Regression
Linear regression was used to model the effect one variable, an explanatory variable, has on another, the response variable. In particular, if one variable changed by some amount, you assumed the other changed by a multiple of that same amount. That multiple being the slope of the regression line. Multiple linear regression does the same, only there are multiple explanatory variables or regressors.There are many situations where intuitively this is the correct model. For example, the price of a new home depends on many factors -- the number of bedrooms, the number of bathrooms, the location of the house, etc. When a house is built, it costs a certain amount for the builder to build an extra room and so the cost of house reflects this. In fact, in some new developments, there is a pricelist for extra features such as $900 for an upgraded fireplace. Now, if you are buying an older house it isn't so clear what the price should be. However, people do develop rules of thumb to help figure out the value. For example, these may be add $30,000 for an extra bedroom and $15,000 for an extra bathroom, or subtract $10,000 for the busy street. These are intuitive uses of a linear model to explain the cost of a house based on several variables. Similarly, you might develop such insights when buying a used car, or a new computer. Linear regression is also used to predict performance. If you were accepted to college, the college may have used some formula to assess your application based on high-school GPA, standardized test scores such as SAT, difficulty of high-school curriculum, strength of your letters of recommendation, etc. These factors all may predict potential performance. Despite there being no obvious reason for a linear fit, the tools are easy to use and so may be used in this manner.
14.1 The model
The standard regression model modeled the response variable yi based on xi as
yi = b0 + b1 xi + ei
where the e are i.i.d. N(0,s2). The task at hand was
to estimate the parameters b0, b1, s2 using the data
(xi,yi). In multiple regression, there are potentially many
variables and each one needs one (or more) coefficients. Again we use
b but more subscripts. The basic model is
yi = b0 + b1 xi1 + b2 xi2 + иии + bp xip + ei
where the e are as before. Notice, the subscript on the
x's involves the ith sample and the number of the variable 1, 2,
..., or p. A few comments before continuing
-
There is no reason that xi1 and xi2 can't be related. In
particular, multiple linear regression allows one to fit quadratic
lines to data such as
yi = b0 + b1 xi + b2 xi2 + ei.
- In advanced texts, the use of linear algebra allows one to write this simply as Y = b X + e where b is a vector of coefficients and the data is (X,Y).
- No function like simple.lm is provided to avoid the model formula notation. There are too many variations available with the formula notation to allow for this.
|
i = b0 + b1 xi1 + иии + bn xip |
If the model is appropriate for the data, statistical inference can be made as before. The estimators, bi (also known as bi), have known standard errors, and the distribution of (bi - bi)/SE(bi) will be the t-distribution with n-(p+1) degrees of freedom. Note, there are p+1 terms estimated these being the values of b0,b1,...,bp.
Example: Multiple linear regression with known answer
Let's investigate the model and its implementation in R with data which we generate ourselves so we know the answer. We explicitly define the two regressors, and then the response as a linear function of the regressors with some normal noise added. Notice, linear models are still solved with the lm function, but we need to recall a bit more about the model formula syntax.
The model formula syntax is pretty easy to use in this case. To add another explanatory variable you just ``add'' it to the right side of the formula. That is to add y we use z ~ x + y instead of simply z ~ x as in simple regression. If you know for sure that there is no intercept term (b0 = 0) as it is above, you can explicitly remove this by adding -1 to the formula
Let's investigate the model and its implementation in R with data which we generate ourselves so we know the answer. We explicitly define the two regressors, and then the response as a linear function of the regressors with some normal noise added. Notice, linear models are still solved with the lm function, but we need to recall a bit more about the model formula syntax.
> x = 1:10
> y = sample(1:100,10)
> z = x+y # notice no error term -- sigma = 0
> lm(z ~ x+y) # we use lm() as before
... # edit out Call:...
Coefficients:
(Intercept) x y
4.2e-15 1.0e+00 1.0e+00
# model finds b_0 = 0, b_1 = 1, b_2 = 1 as expected
> z = x+y + rnorm(10,0,2) # now sigma = 2
> lm(z ~ x+y)
...
Coefficients:
(Intercept) x y
0.4694 0.9765 0.9891
# found b_0 = .4694, b_1 = 0.9765, b_2 = 0.9891
> z = x+y + rnorm(10,0,10) # more noise -- sigma = 10
> lm(z ~ x+y)
...
Coefficients:
(Intercept) x y
10.5365 1.2127 0.7909
Notice that as we added more noise the guesses got worse and
worse as expected. Recall that the difference
between bi and bi is controlled by the standard error of
bi and the standard deviation of bi (which the standard error
estimates) is related to s2 the variance of the ei.
In short, the more noise the worse the confidence, the more data the
better the confidence.The model formula syntax is pretty easy to use in this case. To add another explanatory variable you just ``add'' it to the right side of the formula. That is to add y we use z ~ x + y instead of simply z ~ x as in simple regression. If you know for sure that there is no intercept term (b0 = 0) as it is above, you can explicitly remove this by adding -1 to the formula
> lm(z ~ x+y -1) # no intercept beta_0
...
Coefficients:
x y
2.2999 0.8442
Actually, the lm command only returns the coefficients (and
the formula call) by default. The two methods summary and
anova can yield more information. The output of summary
is similar as for simple regression.
> summary(lm(z ~ x+y ))
Call:
lm(formula = z ~ x + y)
Residuals:
Min 1Q Median 3Q Max
-16.793 -4.536 -1.236 7.756 14.845
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10.5365 8.6627 1.216 0.263287
x 1.2127 1.4546 0.834 0.431971
y 0.7909 0.1316 6.009 0.000537 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 11.96 on 7 degrees of freedom
Multiple R-Squared: 0.8775, Adjusted R-squared: 0.8425
F-statistic: 25.08 on 2 and 7 DF, p-value: 0.000643
First, summary returns the method that was used with
lm, next is a five-number summary of the residuals. As before,
the residuals are available with the residuals command. More
importantly, the regression coefficients are presented in a table
which includes their estimates (under Estimate), their
standard error (under Std. Error), the t-value for a
hypothesis test that bi = 0 under t value and the
corresponding p-value for a two-sided test. Small p-values are
flagged as shown with the 3 asterisks,***, in the y
row. Other tests of hypotheses are easily done knowing the first two
columns and the degrees of freedom. The standard error for the residuals is given along with its
degrees of freedom. This allows one to investigate the residuals
which are again available with the residuals method. The
multiple and adjusted R2 is given. R2 is interpreted as the
``fraction of the variance explained by the model.'' Finally the F
statistic is given. The p-value for this is from a hypotheses test
that b1 = 0 = b2 = иии = bp. That is, the
regression is not appropriate. The theory for this comes
from that of the analysis of variance (ANOVA).
Example: Sale prices of homes
The homeprice dataset contains information about homes that sold in a town of New Jersey in the year 2001. We wish to develop some rules of thumb in order to help us figure out what are appropriate prices for homes. First, we need to explore the data a little bit. We will use the lattice graphics package for the multivariate analysis. First we define the useful panel.lm function for our graphs.
Next, let's find the coefficients for the model. If you are still unconvinced that the linear relationships are appropriate, you might try some more plots. The pairs(homeprice) command gives a good start.
We'll begin with the regression on bedrooms and neighborhood.
Next, we know that home buyers covet bathrooms. Hence, they should add value to a house. How much?
To test this we will do a formal hypothesis test -- a one-sided test to see if this b is 15 against the alternative it is greater than 15.
Before rushing off to buy or sell a home, try to do some of the problems on this dataset.
The homeprice dataset contains information about homes that sold in a town of New Jersey in the year 2001. We wish to develop some rules of thumb in order to help us figure out what are appropriate prices for homes. First, we need to explore the data a little bit. We will use the lattice graphics package for the multivariate analysis. First we define the useful panel.lm function for our graphs.
> library(lattice);data(homeprice);attach(homeprice)
> panel.lm = function(x,y) {
+ panel.xyplot(x,y)
+ panel.abline(lm(y~x))}
> xyplot(sale ~ rooms | neighborhood,panel= panel.lm,data=homeprice)
## too few points in some of the neighborhoods, let's combine
> nbd = as.numeric(cut(neighborhood,c(0,2,3,5),labels=c(1,2,3)))
> table(nbd) # check that we partitioned well
nbd
1 2 3
10 12 7
> xyplot(sale ~ rooms | nbd, panel= panel.lm,layout=c(3,1))
The last graph is plotted in figure 53. We compressed the neighborhood variable as the data was to thinly spread out. We kept it numeric using as.numeric as cut returns a factor. This is not necessary for R to do the regression, but to fit the above model without modification we need to use a numeric variable and not a categorical one. The figure shows the regression lines for the 3 levels of the neighborhood. The multiple linear regression model assumes that the regression line should have the same slope for all the levels.
Next, let's find the coefficients for the model. If you are still unconvinced that the linear relationships are appropriate, you might try some more plots. The pairs(homeprice) command gives a good start.
We'll begin with the regression on bedrooms and neighborhood.
> summary(lm(sale ~ bedrooms + nbd))
...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -58.90 48.54 -1.213 0.2359
bedrooms 35.84 14.94 2.400 0.0239 *
nbd 115.32 15.57 7.405 7.3e-08 ***
This would say an extra bedroom is worth $35 thousand, and a better
neighborhood $115 thousand. However, what does that negative
intercept mean? If there are 0 bedrooms (a small house!) then the
house is worth
> -58.9 + 115.32*(1:3) # nbd is 1, 2 or 3 [1] 56.42 171.74 287.06This is about correct, but looks funny.
Next, we know that home buyers covet bathrooms. Hence, they should add value to a house. How much?
> summary(lm(sale ~ bedrooms + nbd + full))
...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -67.89 47.58 -1.427 0.1660
bedrooms 31.74 14.77 2.149 0.0415 *
nbd 101.00 17.69 5.709 6.04e-06 ***
full 28.51 18.19 1.567 0.1297
...
That is $28 thousand dollars per full bathroom. This seems a little high, as the
construction cost of a new bathroom is less than this. Could it
possibly be $15 thousand?To test this we will do a formal hypothesis test -- a one-sided test to see if this b is 15 against the alternative it is greater than 15.
> SE = 18.19 > t = (28.51 - 15)/SE > t [1] 0.7427158 > pt(t,df=25,lower.tail=F) [1] 0.232288We accept the null hypothesis in this case. The standard error is quite large.
Before rushing off to buy or sell a home, try to do some of the problems on this dataset.
Example: Quadratic regression
In 1609 Galileo proved that the trajectory of a body falling with a horizontal component is a parabola.15 In the course of gaining insight into this fact, he set up an experiment which measured two variables, a height and a distance, yielding the following data
Our modern eyes, now expect parabolas. Let's see if linear regression can help us find the coefficients.
In 1609 Galileo proved that the trajectory of a body falling with a horizontal component is a parabola.15 In the course of gaining insight into this fact, he set up an experiment which measured two variables, a height and a distance, yielding the following data
In plotting the data, Galileo apparently saw the parabola and with this insight proved it mathematically.
height (punti) 100 200 300 450 600 800 1000 dist (punti) 253 337 395 451 495 534 574
Our modern eyes, now expect parabolas. Let's see if linear regression can help us find the coefficients.
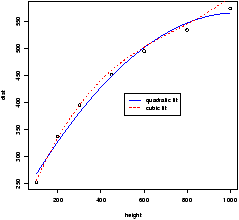
> dist = c(253, 337,395,451,495,534,574) > height = c(100,200,300,450,600,800,1000) > lm.2 = lm(dist ~ height + I(height^2)) > lm.3 = lm(dist ~ height + I(height^2) + I(height^3)) > lm.2 ... (Intercept) height I(height^2) 200.211950 0.706182 -0.000341 > lm.3 ... (Intercept) height I(height^2) I(height^3) 1.555e+02 1.119e+00 -1.254e-03 5.550e-07Notice we need to use the construct I(height2), The I function allows us to use the usual notation for powers. (The ^ is used differently in the model notation.) Looking at a plot of the data with the quadratic curve and the cubic curve is illustrative.
> quad.fit = 200.211950 + .706182 * pts -0.000341 * pts^2
> cube.fit = 155.5 + 1.119 * pts - .001234 * pts^2 + .000000555 * pts^3
> plot(height,dist)
> lines(pts,quad.fit,lty=1,col="blue")
> lines(pts,cube.fit,lty=2,col="red")
> legend(locator(1),c("quadratic fit","cubic fit"),lty=1:2,col=c("blue","red"))
All this gives us figure 54.
Both curves seem to fit well. Which to choose? A hypothesis test of b3 = 0 will help decide between the two choices. Recall this is done for us with the summary command
> summary(lm.3)
...
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.555e+02 8.182e+00 19.003 0.000318 ***
height 1.119e+00 6.454e-02 17.332 0.000419 ***
I(height^2) -1.254e-03 1.360e-04 -9.220 0.002699 **
I(height^3) 5.550e-07 8.184e-08 6.782 0.006552 **
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
...
Notice the p-value is quite small (0.006552) and so is flagged
automatically by R. This says the null hypothesis (b3=0)
should be rejected and the alternative (b3 ╣ 0) is accepted.
We are tempted to attribute this cubic presence to resistance which
is ignored in the mathematical solution which finds the quadratic
relationship.
Some Extra Insight: Easier plotting
To plot the quadratic and cubic lines above was a bit of typing. You might expect the computer to do this stuff for you. Here is an alternative which can be generalized, but requires much more sophistication (and just as much typing in this case)
To plot the quadratic and cubic lines above was a bit of typing. You might expect the computer to do this stuff for you. Here is an alternative which can be generalized, but requires much more sophistication (and just as much typing in this case)
> pts = seq(min(height),max(height),length=100) > makecube = sapply(pts,function(x) coef(lm.3) %*% x^(0:3)) > makesquare = sapply(pts,function(x) coef(lm.2) %*% x^(0:2)) > lines(pts,makecube,lty=1) > lines(pts,makesquare,lty=2)The key is using the function which takes the coefficients returned by coef and ``multiplies'' (%*%) by the appropriate powers of x, namely 1,x,x2 and x3. Then this function is applied to each value of pts using sapply which finds the value of the function for each value of pts.
14.2 Problems
- 14.1
- For the homeprice dataset, what does a half bathroom do for the sale price?
- 14.2
- For the homeprice dataset, how do the coefficients change if you force the intercept, b0 to be 0? (Use a -1 in the model formula notation.) Does it make any sense for this model to have no intercept term?
- 14.3
- For the homeprice dataset, what is the effect of neighborhood on the difference between sale price and list price? Do nicer neighborhoods mean it is more likely to have a house go over the asking price?
- 14.4
- For the homeprice dataset, is there a relationship between houses which sell for more than predicted (a positive residual) and houses which sell for more than asking? (If so, then perhaps the real estate agents aren't pricing the home correctly.)
- 14.5
- For the babies dataset, do a multiple regression of birthweight with regressors the mothers age, weight and height. What is the value of R2? What are the coefficients? Do any variables appear to be 0?
Copyright © John Verzani, 2001-2. All rights reserved.